DIRT Report

Appendix B: Trending Regression Analysis

Objective

The objective of this analysis is to assess whether damage counts are changing significantly[1] over time in the United States after accounting for several potential driving factors (e.g., economic growth).

Method

As in past years, regression analysis was used to relate damage counts by month and state to a set of explanatory variables including factors related to the economy, demographics, dig activity, etc. However, for the current analysis focused on trends over time year variables were added to account for changes over the different years included in the analysis (2020 to 2022).

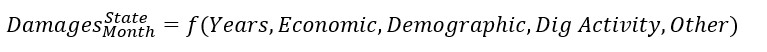
Given that the damage data are structured as count data, Poisson and negative binomial count models were used for the analysis. Both models are typically used to estimate count data, but the negative binomial model relaxes a key assumption of the Poisson model (via an overdispersion parameter). Non-panel models were run with robust standard errors clustered on the geographic unit (state) which account for the panel nature of the data.

For this year’s analysis, we also took a step back and ran count models at the level of the country (Equation 2). This overcomes certain limitations of models at the state level, such as noise introduced by variation in damage counts resulting from how the data was assembled (e.g., the subset of consistent companies may not properly represent all states leading to variation across states not representative of actual damage activity). However, other limitations present themselves at this scale including that so few observations may increase multicollinearity and results may still be skewed towards states which are better represented in the assembled dataset. Furthermore, data on certain variables is only collected at annual timescales meaning that these variables cannot be included in the regression analysis due to multicollinearity (e.g., One Call transmissions or PHMSA data).

This relationship was modeled following procedures similar to those used for the state level analysis. Poisson and negative binomial count models were used both estimated with robust standard errors.

The coefficients of interest for the trend analyses are those on variables representing the years in Equations 1 or 2. If these coefficients are significantly different from zero after accounting for the other factors in this equation, then damage counts are changing over time for reasons other than the factors incorporated into the model. Before running the regression models, multicollinearity between variables was assessed using variance inflation factors (VIF). Since multicollinearity can influence how regression coefficients for certain variables are interpreted, highly collinear variables were iteratively removed according to their VIF using a VIF threshold of 5. This resulted in the primary models having a reduced set of variables with limited collinearity and regression analyses were conducted on this reduced set as well as the total set of variables.

Data

In consultation with CGA staff a subset of the United States damage data was assembled for the 2020 to 2022 period. To help reduce the noise in the data stemming from variations in company reporting behavior from year to year rather than actual changes in damages, the damage count dataset was initially assembled from companies that reported more than 1000 damages at least once annually from 2020 to 2022. Since this dataset was skewed toward natural gas and One Call center stakeholders it was enhanced with damage counts from the electric, telecom/CATV, excavator, and water stakeholders.  

For the state level analyses, damages in the final set of data were distributed across the 50 states and the District of Columbia as well as the 36 months over the 2020 to 2022 period. Damage counts reported for certain states are zero or very low and are thus not well represented in the analysis (i.e., Alaska, Hawaii, Maine, Rhode Island, Vermont, and West Virginia). These states were omitted from the analyses reported below (although the results are very similar when they included). However, reported damage counts in other states may be lower than expected due to limitations in how the dataset was assembled (e.g., a state could have lower counts if there are relatively few consistently reporting companies operating in the state). As such a separate variable, the ratio of total annual damage counts and total annual 811 Center transmissions for a state, was incorporated as an attempt to account for count data being poorly represented for certain states. Data on other variables, including weather, demographics, economics (e.g., GDP or employment), construction, dig activity (e.g., transmissions), as well as PHMSA data on damages and tickets were also collected (Table 1). Similar data were used for the analyses at the national level although at a different scale (e.g., damages were only distributed across the 36-month period).

Results and Conclusion

The initial multicollinearity check revealed that many of the variables in Table 1 were highly collinear, especially for the analysis at the national scale, and these variables were removed from the regression analysis. However, the variables of interest, year _2021 and year_2022 were not substantially correlated with the other explanatory variables in the model.

For the models at the state level, the results are different from last year’s analysis for the period 2019 to 2020. The results of both the Poisson and negative binomial models indicate that damage counts in 2021 and 2022 do not differ significantly from those in 2020 (Table 2). Further testing on the results of the Poisson model results, specifically testing whether the coefficients on the year_2021 and year_2022 variables differ, suggests that damage counts in 2022 also do not differ significantly from those in 2021 (at the 1% level of significance). However, similar testing on the results of the negative binomial model indicate that damage counts in 2022 do differ significantly from counts in 2021 although only at the 10% level of significance. Note that the negative binomial model is preferred given that the dispersion parameter (alpha) is not zero. In addition, follow-up testing of the Poisson model suggests that this model is not appropriate for the data (Deviance and Pearson statistics).

Results were similar at the national scale as none of the coefficients on the year variables were significant (Table 3). Further testing on whether the coefficients on the year_2021 and year_2022 variables differ indicates that they differ significantly at the 5% level of significance. These results hold for both the Poisson and negative binomial models, although the deviance and Pearson statistics suggest that the negative binomial model is preferred.

Assuming that the assembled data is representative of trends in all sectors and parts of the United States the models provide evidence that damage counts in 2021 or 2022 do not differ significantly from those in 2020 after accounting for key driving factors. However, there is some evidence that damage counts in 2022 may differ significantly from those in 2021 (counts in 2022 may be higher). Findings are similar at the national level. Caution is advised when interpreting these conclusions since it is not possible to verify the assumption that the dataset is representative.

Tables

Table 1: Variables Initially Used in the Regression Analysis

Table 2: Count Models Relating Damages to Explanatory Variables with Standard Errors Clustered on Geography as Well as the Fixed Effects Poisson Model^a

^a Cells contain model coefficients and associated standard errors in round brackets.

***, **, and * indicate that the coefficient is significantly different from zero at the 1%, 5%, and 10% level of significance

Table 3: National Scale Count Models Relating Damages to Explanatory Variables with Robust Standard Errors^a

^a Cells contain model coefficients and associated standard errors in round brackets.

***, **, and * indicate that the coefficient is significantly different from zero at the 1%, 5%, and 10% level of significance